Вопросы эффективности вычислений
Рассмотрим проблему ускорения вычислений в одной из самых трудоемких операций компьютерной графики – операции поворота точки относительно начала координат. Как было показано ранее, для ее выполнения необходимо произвести 4 операции умножения, 2 операции сложения, а также вычислить значения синуса и косинуса угла поворота. Напомним вид формул поворота:


Одним из наиболее часто встречающихся способов ускорения операции поворота является отказ от вычисления синуса и косинуса угла во время выполнения программы, и использование их заранее подсчитанных значений, которые занесены в специальную таблицу. Например, в этой таблице могут храниться значения синусов и косинусов углов поворота с шагом в 1 градус. Тогда целое количество градусов угла поворота может служить в качестве индекса при извлечении соответствующих значений синусов и косинусов из таблицы. Такой прием называется табличным поворотом.
Дополнительным способом ускорения операции поворота является уменьшение количества операций умножения. Рассмотрим вывод формулы О. Бьюнемана с использованием тангенса половинного угла, в которой поворот точки вокруг начала координат производится за 3 операции умножения и 3 операции сложения. Так как на многих микропроцессорах операции умножения выполняются дольше чем операции сложения, то экономия времени достигается за счет уменьшения операций умножения.
Вывод формулы будем получать из геометрических построений, как показано на рис.27.
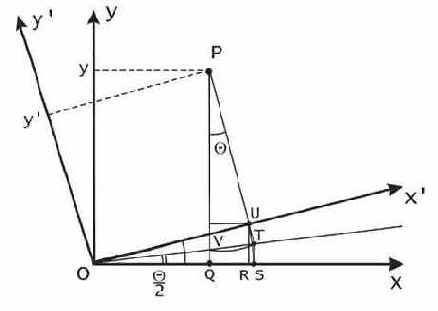
Рис. 27. Вывод формулы О. Бьюнемана.
Будем искать выражение координат




























Последние три равенства будем называть формулой Бьюнемана.
