Проецирование трехмерных объектов
Рассмотрим проблему показа трехмерных изображений на двумерной плоскости. Для этого необходимо иметь определенные математические модели. В этих моделях должны учитываться различные факторы, влияющие на визуальное восприятие человеком реальных образов. Способ перехода от трехмерных объектов к их изображениям на плоскости будем называть проекцией. Далее рассматриваются различные виды проекций.
Для того, чтобы увидеть на плоскости монитора трехмерное изображение нужно уметь задать способ отображения трехмерных точек в двумерные. Сделать это можно, вообще говоря, по-разному. В общем случае проекции преобразуют точки, заданные в системе координат размерностью n в точки системы координат размерностью меньшей, чем n. В нашем случае точки трехмерного пространства преобразуются в точки двумерного пространства. Проекции строятся с помощью проецирующих лучей или проекторов, которые выходят из точки, которая называется центром проекции. Проекторы проходят через плоскость, которая называется проекционной или картинной плоскостью и затем проходят через каждую точку трехмерного объекта и образуют тем самым проекцию. Тип проецирования на плоскую, а не искривленную поверхность, где в качестве проекторов используются прямые. а не искривленные линии, называется плоской геометрической проекцией. Плоские геометрические проекции делятся на два вида: центральные и параллельные. Если центр проекции находится на конечном расстоянии от проекционной плоскости, то проекция – центральная. Если же центр проекции удален на бесконечность, то проекция – параллельная.
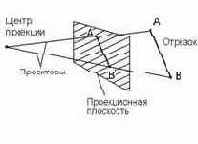
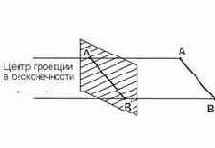
Рис. 14. Центральная проекция. Рис. 15. Параллельная проекция.
Точкой схода называется точка пересечения центральных проекций любой совокупности параллельный прямых, которые не параллельны проекционной плоскости. Существует бесконечное множество точек схода. Точка схода называется главной если совокупность прямых параллельна одной из координатных осей. В зависимости от того, сколько координатных осей пересекает проекционную плоскость различают одно-, двух- и трехточечные проекции.
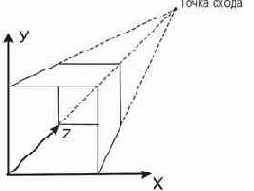
Рис. 16. Одноточечная проекция.
Простейшей является параллельная прямоугольная проекция. В ней совместно изображаются виды сверху, спереди и сбоку. Эти проекции часто используются в черчении. В зависимости от соотношения между направлениями проецирования и нормалью к проекционной плоскости параллельные проекции разделяются на ортографические или ортогональные, в которых эти направления совпадают, и косоугольные, в которых они не совпадают. В зависимости от положения осей системы координат объекта относительно проекционной плоскости ортографические проекции делятся на аксонометрические и изометрические. В изометрических проекциях оси системы координат составляют одинаковые углы с проекционной плоскостью. В аксонометрических проекциях эти углы разные. Центральная перспективная проекция приводит к визуальному эффекту, подобному тому, который дает зрительная система человека. При этом наблюдается эффект перспективного укорачивания, когда размер проекции объекта изменяется обратно пропорционально расстоянию от центра проекции до объекта. В параллельных проекциях отсутствует перспективное укорачивание, за счет чего изображение получается менее реалистичным и параллельные прямые всегда остаются параллельными.
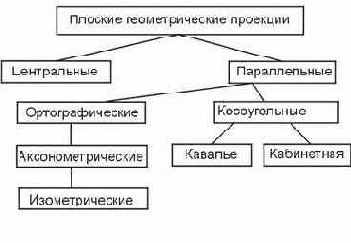
Рис. 17. Типы проекций.
Рассмотрим более подробно центральную перспективную проекцию с математической точки зрения. Для получения формул центральной перспективной проекции расположим оси системы координат, проекционную плоскость и центр проекции как показано на рис. 18.

Рис. 18. Расположение осей координат на экране.
Будем имитировать на экране то, что как будто бы реально находится в пространстве за ним. Заметим, что получилась левосторонняя система координат. Будем считать что плоскость экрана монитора совпадает с проекционной плоскостью. Прежде чем переходить к собственно вычислениям следует сделать одно важное замечание. Поскольку поверхность любого трехмерного объекта содержит бесконечное число точек, то необходимо задать способ описания поверхности объекта конечным числом точек для представления в компьютере.
А именно, будем использовать линейную аппроксимацию объектов в трехмерном пространстве с помощью отрезков прямых и плоских многоугольников. При этом отрезки прямых после перспективного преобразования переходят в отрезки прямых на проекционной плоскости. Доказательство этого достаточно простое и здесь не приводится. Это важное свойство центральной перспективы позволяет проецировать, т.е. производить вычисления только для конечных точек отрезков, а затем соединять проекции точек линиями уже на проекционной плоскости.
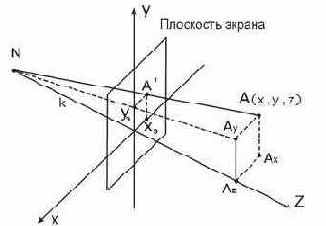
Рис. 19. Вывод формул центральной перспективной проекции.
Точка








аналогично для x:

Напомним, что k -это расстояние, а наблюдатель находится в точке

Если точку наблюдения поместить в начало координат, а проекционную плоскость на расстояние





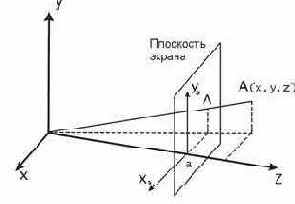
Рис. 20. Другой способ вычисления координат точек в центральной перспективной проекции.
Формулы (1) более удобны при необходимости простым образом приближать или удалять наблюдателя от проекционной плоскости. Формулы (2) требуют меньше времени для вычислений за счет отсутствия операции сложения.
Рассмотрим далее некоторые факторы. влияющие на восприятие человеком трехмерности. Одним из простых способов представления трехмерных объектов являются так называемые проволочные изображения. Кривые линии при этом апроксимируются отрезками прямых. Это наиболее быстрый и простой способ изображения.
Для усиления эффекта трехмерной глубины в проволочных изображениях объектов удаляют невидимые линии. Линии или их части, закрытые поверхностями объекта, не изображаются. Для этого применяется специальный алгоритм, что требует уже больших вычислений.
Передача глубины может осуществляться изменением уровня яркости. Объекты, которые находятся ближе к наблюдателю, изображаются ярче, чем те, которые расположены дальше от него. Движение объектов также дает дополнительный эффект глубины. Например, вращение объектов вокруг вертикальной оси позволяет отличить точки, находящиеся на разном расстоянии от оси за счет различия линейной скорости вращения точек. Это так называемый кинетический или динамический эффект глубины.
Более тонко трехмерность объектов может быть представлена за счет различий отражательных способностей поверхностей, их рельефа и текстуры, а также расчета теней, отбрасываемых поверхностями объекта. Одним из редко используемых, но наиболее эффективных способов достижения эффекта трехмерности является стереоскопия. При этом отдельно для правого и левого глаза наблюдателя формируются изображения, которые незначительно отличаются друг от друга, подобно тому, как это происходит в реальности. Это вызывает так называемый бинокулярный эффект, который заключается в том, что наш мозг сливает два отдельных образа в один, интерпретируемый как трехмерный. Эти два раздельных изображения называются стереопарой.
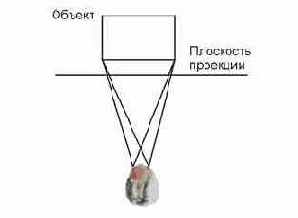
Рис. 21. Бинокулярный эффект, стереоскопия.
Технически этот метод реализуется, например, с помощью очков со специальными поляризованными стеклами. На экран монитора поочередно выводятся изображения для левого и правого глаза. А стекла очков становятся поочередно, соответственно, прозрачными или непрозрачными. При достаточно частой смене изображений смены состояний прозрачности и непрозрачности не ощущается. Поскольку при изменении положения головы центр проекции остается на месте, то создается псевдо-трехмерный эффект. Синхронизация смены кадров на экране и поляризации линз очков происходит с помощью специальных датчиков, расположенных на очках и мониторе.
