Двумерные матричные преобразования

Рассмотрим преобразования координат точек на плоскости. На рис. 22   точка

 перенесена в точку .

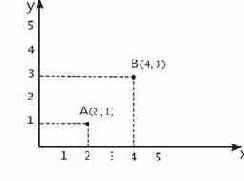
Рис. 22. Операция переноса или трансляции точки

 в точку .

 Математически этот перенос можно описать с помощью вектора переноса

. Пусть  радиус вектор, соответствующий вектору переноса . Тогда переход из точки  в точку  будет соответствовать векторной записи . Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:

Масштабированием объектов называется растяжение объектов вдоль соответствующих осей координат относительно начала координат. Эта операция применяется к каждой точке объекта, поэтому можно также говорить о масштабировании точки. При этом, конечно, речь не идет об изменении размеров самой точки. Масштабирование достигается умножением координат точек на некоторые константы. В том случае, когда эти константы равны между собой, масштабирование называется однородным. На рис.23 приведен пример однородного масштабирования треугольника

.

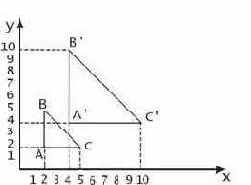
Рис. 23. Операция масштабирования .

 После применения операции однородного масштабирования с коэффициентом 2 он переходит в треугольник

. Обозначим матрицу масштабирования . Для точек  и  операция масштабирования в матричном виде будет выглядеть следующим образом:

 .

Рассмотрим далее операцию вращения точки на некоторый угол относительно начала координат. На рисунке 24 точка

 переходит в точку  поворотом на угол .

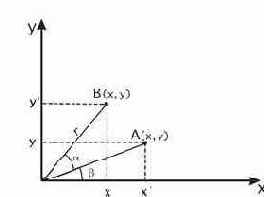
Рис. 24. Операция поворота точки

на угол .

Найдем преобразование координат точки А в точку В. Обозначим

 угол, который составляет радиус-вектор  с осью Оx. Пусть r – длина радиус-вектора , тогда

Так как

 и , то подставляя эти выражения в уравнения для  и , получаем:

 

В матричном виде вращение точки А на угол

 выглядит следующим образом:               

Содержание раздела

---

---