Алгоритмы удаления невидимых ребер и граней
Алгоритмы удаления невидимых граней могут быть условно поделены на два класса в зависимости от принципов, заложенных для их реализации. Первый класс – это алгоритмы работающие в пространстве объекта. Это означает, что для определения видимости данной грани сравнивается ее взаимное расположение со всеми остальными гранями в трехмерной сцене. Пусть N – количество граней в трехмерной сцене. Для построения трехмерной сцены в этом случае необходимо сравнить положение каждой грани с оставшимися, что требует порядка


Другой класс алгоритмов - работающих в пространстве изображения, основан на нахождении точки ближайшей грани которую пересекает луч зрения, проходящий через заданную точку на растре. Поскольку число точек на растровом экране фиксировано, то алгоритмы этого класса менее чувствительны к увеличению количества объектов в трехмерной сцене. Пусть n - число точек на растровом экране. Тогда количество операций, необходимых для построения трехмерной сцены будет порядка




Рассмотрим алгоритм удаления невидимых граней с использованием
z-буфера, который является одним из наиболее часто используемых в современных приложениях компьютерной графики. Он работает в пространстве изображения и применяется в таких популярных графических библиотеках как OpenGL и Direct3D.
Алгоритм работает в параллельной проекции. Пусть размеры окна вывода или экрана составляют X
точек в ширину и Y
точек в высоту. В качестве z-буфера заведем двумерный прямоугольный массив чисел по размерности совпадающий с окном вывода или экрана, т.е. X

В начале работы алгоритма в z-буфер заносятся значения, соответствующие бесконечности.
Реализация пунктов 1 и 3 достаточно очевидна. Рассмотрим подробнее пункт 2.
Пусть многоугольник P после упорядочения находится в конце списка, то есть является наиболее удаленным. Все многоугольники Q чьи оболочки перекрываются с z-оболочкой P должны проходить проверку по пяти тестам (шагам). Если на некотором шаге получен утвердительный ответ, то P сразу преобразуется в растровую форму.
Пять тестов:
1. x-Оболочки многоугольников не перекрываются, поэтому сами многоугольники тоже не перекрываются.
2. y-Оболочки многоугольников не перекрываются, поэтому сами многоугольники тоже не перекрываются.
3. P полностью расположен с той стороны от плоскости Q, которая дальше от точки зрения (этот тест дает положительный ответ как показано на рис. 36 а).
4. Q полностью расположен с той стороны от плоскости P, которая ближе к точке зрения. Этот тест дает положительный ответ как показано на рис. 36 b).
5. Проекции многоугольников на плоскости xOy, то есть на экране, не перекрываются (это определяется сравнением ребер одного многоугольника с ребрами другого).
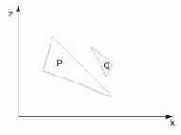
Рис. 35.

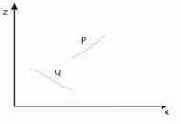
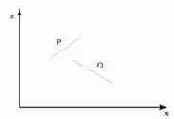
а) b)
Рис. 36. Взаимные расположения треугольников в пространстве.
Если во всех пяти тестах получен отрицательный ответ, то P – действительно закрывает Q. Тогда меняем P и Q в списке местами. В случае, как показано на рис. 37, алгоритм зацикливается.
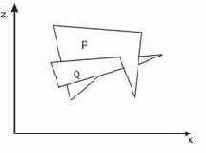
Рис. 37.
Для избежания зацикливания вводится ограничение: многоугольник, перемещенный в конец списка (т.е. помеченный), не может быть повторно перемещен. Вместо этого многоугольник P или Q разделяется плоскостью другого на два новых многоугольника. Эти два новых многоугольника включаются в соответствующие места упорядоченного списка, и алгоритм продолжает работу.
В отличие от универсальных алгоритмов узкоспециализированный алгоритм удаления невидимых граней выпуклых тел позволяет производить вычисления гораздо быстрее.Он работает для центральной перспективной проекции. Рассмотрим работу этого алгоритма на примере как изображено на рис. 38.
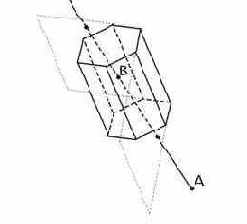
Рис. 38. Пересечения прямой AB с плоскостями граней призмы.
Пусть наблюдатель находится в точке A. Выберем точку B, которая заведомо является внутренней для выпуклой фигуры, в данном случае призмы. Выберем некоторую грань, про которую мы хотим узнать видима она из точки A, или не видима. Построим плоскость, в которой лежит выбранная грань. Найдем точку пересечения плоскости и прямой, которая образована отрезком AB. Если точка пересечения прямой и плоскости лежит внутри отрезка AB, то делаем вывод, что данная грань видима. Если точка пересечения находится вне отрезка AB, то грань не видима. В случае, когда прямая и плоскость параллельны, считаем что грань не видима.
