Алгоритмы растровой графики
Растром называется прямоугольная сетка точек, формирующих изображение на экране компьютера. Каждая точка растра характеризуется двумя параметрами: своим положением на экране и своим цветом, если монитор цветной, или степенью яркости, если монитор черно-белый. Поскольку растровые изображения состоят из множества дискретных точек, то для работы с ними необходимы специальные алгоритмы. Рисование отрезка прямой линии - одна из простейших задач растровой графики. Смысл ее заключается в вычислении координат пикселов, находящихся вблизи непрерывных отрезков, лежащих на двумерной растровой сетке.
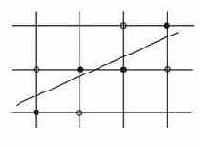
Рис. 28. Растеризация отрезка прямой линии.
Термин “пиксел” образован от английского pixel (picture element - элемент изображения) - то есть точка на экране. Будем считать, что пикселы имеют целочисленные координаты. На первый взгляд кажется, что эта задача имеет простое решение. Пусть конечные точки отрезка имеют целочисленные координаты, и уравнение прямой, содержащей отрезок:











Когда








Для вывода формул алгоритма Брезенхема рассмотрим рис. 29.
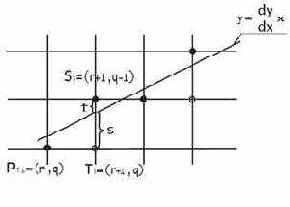
Рис. 29. Рисование отрезков прямых по методу Брезенхема.
Пусть начало отрезка имеет координаты

























Поскольку знак






Пусть на предыдущем шаге






Осталось узнать как вычислить




Далее приводится листинг процедуры на языке Паскаль, реализующей алгоритм Брезенхема.
Procedure Bresenham(x1,y1,x2,y2,Color: integer);
var
dx,dy,incr1,incr2,d,x,y,xend: integer;
begin
dx:= ABS(x2-x1);
dy:= Abs(y2-y1);
d:=2*dy-dx; {начальное значение для d}
incr1:=2*dy; {приращение для d<0}
incr2:=2*(dy-dx); {приращение для d>=0}
if x1>x2 then {начинаем с точки с меньшим знач. x}
begin
x:=x2;
y:=y2;
xend:=x1;
end
else
begin
x:=x1;
y:=y1;
xend:=x2;
end;
PutPixel(x,y,Color); {первая точка отрезка}
While x<xend do
begin
x:=x+1;
if d<0 then
d:=d+incr1 {выбираем нижнюю точку}
else
begin
y:=y+1;
d:=d+incr2; {выбираем верхнюю точку, y-возрастает}
end;
PutPixel(x,y,Color);
end;{while}
end;{procedure}
Перед тем, как исследовать методы получения изображений более сложных, чем отрезки прямых, рассмотрим проблему, незримо присутствующую в большинстве задач компьютерной графики. Эта проблема отсечения изображения по некоторой границе, например, по границе экрана, или, в общем случае, некоторого прямоугольного окна. Рассмотрим эту задачу применительно к отрезкам прямых. Некоторые из них полностью лежат внутри области экрана, другие целиком вне ее, а некоторые пересекают границу экрана.
Правильное отображение отрезков означает нахождение точек пересечения их с границей экрана и рисование только тех их частей, которые попадают на экран. Один из очевидных способов отсечения отрезков состоит в определении точек пересечения прямой, содержащей отрезок, с каждой из четырех прямых, на которых лежат границы окна и проверки не лежит ли хотя бы одна точка пересечения на границе. В этом случае для каждой пары сторона-отрезок необходимо решать систему из двух уравнений, используя операции умножения и деления. При этом удобно параметрическое задание прямых:


Для






Рассмотрим алгоритм Коэна-Сазерленда для отсечения отрезков прямых. Этот алгоритм позволяет легко определять нахождение отрезка полностью внутри или полностью снаружи окна, и если так, то его можно рисовать или не рисовать, не заботясь об отсечении по границе окна.
Для работы алгоритма вся плоскость в которой лежит окно разбивается на девять подобластей или квадрантов, как показано на рис. 30.
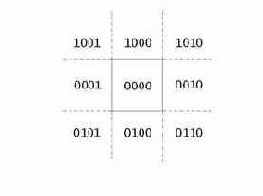
Рис. 30. Разбиение на подобласти в методе Коэна-Сазерленда.
Окну соответствует область обозначенная кодом 0000. Конечным точкам отрезка приписывается 4-битный код “вне/внутри” в зависимости от нахождения отрезка в соответствующей подобласти. Каждому биту присваивается значение 1 в соответствии со следующим правилом.
Бит 1 - точка находится выше окна;
Бит 2 – точка находится ниже окна;
Бит 3 - точка находится справа от окна;
Бит 4 - точка находится слева от окна;
Иначе биту присваивается нулевое значение. Значения этих битов для конечных точек отрезков легко определить по знакам соответствующих разностей:






Отрезок отбрасывается без вычислений если оба его конца находятся выше, ниже, правее или левее окна. В этих случаях соответствующие биты в обоих кодах равны 1 и это легко определить, умножив эти коды по бинарной операции И. Если результат операции И равен 0000, то отрезок нельзя ни принять ни отбросить, так как он может пересекаться с окном. В этом случае применяется последовательное разделение отрезка, так что на каждом шаге конечная точка отрезка с ненулевым кодом вне/внутри заменяется на точку, лежащую на стороне окна или на прямой содержащей сторону. При этом порядок перебора сторон окна не имеет значения.
Далее приводится текст процедуры на языке Паскаль, с довольно изящной реализацией этого метода. Отрезок задан граничными точками


Procedure CLIP(x1,x2,y1,y2,xmin,xmax,ymin,ymax: real);
type
outcode = array[1..4] of boolean;
var
accept,reject,done: boolean;
outcode1,outcode2,
outcode3,outcode4:outcode;{коды вне/внутри}
begin
accept:= false;
reject:= false;
done:= false;
repeat
Outcodes(x1,y1,outcode1);
Outcodes(x2,y2,outcode2);
{проверка на отбрасывание}
reject:=Reject_Check(outcode1,outcode2);
if reject then done:= true
else
begin {возможно принятие целиком}
accept:=Accept_Check(outcode1,outcode2);
if accept then done:=true
else
begin {разделить отрезок}
{если P1
внутри, то с помощью SWAP
сделать снаружи}
if not((outcode1[1])or(outcode1[2])or
(outcode1[3])or(outcode1[4])) then SWAP;
{теперь P1
перемещается в точку пересечения}
if outcode1[1] then
begin {отбросить верхнюю часть}
x1:=x1+(x2-x1)*(ymax-y1)/(y2-y1);
y1:=ymax;
end
else if outcode1[2] then
if outcode1[1] then
begin {отбросить нижнюю часть}
x1:=x1+(x2-x1)*(ymin-y1)/(y2-y1);
y1:=ymin;
end
else if outcode1[3] then
begin {отбросить правую часть}
y1:=x1+(y2-y1)*(ymax-x1)/(x2-x1);
x1:=xmax;
end
else if outcode1[4] then
begin {отбросить левую часть}
y1:=x1+(y2-y1)*(ymin-x1)/(x2-x1);
x1:=xmin;
end;
end;
end;
until done;
if accept then
Line(x1,y1,x2,y2); {нарисовать отрезок}
end;{procedure}
