ОСНОВЫ КОМПОЗИЦИИ В ПРИКЛАДНОЙ ГРАФИКЕ
Понятие о гармонии
4. ПОНЯТИЕ О ГАРМОНИИ МАТЕМАТИЧЕСКОЕ
ЗАКОНОМЕРНОСТИ КОМПОЗИЦИИ
Еще в глубокой древности человеком было обнаружено, что все явления в природе связаны друг с другом, что все пребывает в непрерывном дви-жении, изменении, и, будучи выражено числом, обнаруживает удивительные закономерности. В Древней Греции эпохи классики возник ряд учений о гармонии. Из них наиболее глубокий след в мировой культуре оставило Пифагорейское учение. Последователи Пифагора представляли мир, вселенную, космос, природу и человека как единое целое, где все взаимосвязано и находится в гармонических отношениях. Гармония здесь выступает как начало порядка - упорядочивания хаоса. Гармония присуща природе и искусству. "Одни и те же законы существуют для музыкальных ладов и планет". Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено, что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание). Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что в основе мироздания лежат симметричные геометрические формы.
Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую "Канон". Все классическое искусство Греции носит печать пифагорейского учения о пропорциях. Его влияние испытали на себе ученые средневековья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневековый ученый Августин назвал красоту "числовым равенством", философ-схоласт Бонавентура писал: "Красоты и наслаждения нет без пропорциональности, пропорциональность же, прежде всего, существует в числах. Необходимо, чтобы все поддавалось счислению". Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: "Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона по знает ученый".
Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.
Пропорция означает равенство двух или нескольких отношений. Существует несколько видов пропорциональности: математическая, гармоническая, геометрическая и др. В математической равенство двух отношений выражается формулой a:b=c:d, и каждый член ее может быть определен через остальные три. В гармонической пропорции 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например а:с=(а - в):(в - с).
В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с. Разновидностьо геометрической пропорции является пропорция так называемого "золотого сечения", имеющая всего два члена - "а" и "в" - излюбленная пропорция художников, которую в эпоху Возрождения называли "божественной пропорцией".
Золотое сечение (з. с.). Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е., а:в=в:(а -в). Отношение з. с. выражается числом 0,618. Пропорция з. с. 1:0,618= 0,618:0,382.
Если, отрезок прямой выразить через единицу, а затем разделить его на два отрезка по з. с., то больший отрезок будет равен 0,618, а меньший 0,382. На рис. 7 показано деление отрезка на части по золотому сечению.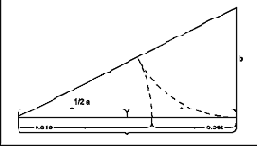
На основании пропорции з. с. был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к О,б18, то есть, к отношению з. с. Пропорции з. с. ученые связывают с развитием органической материи. з. с. было обнаружено в объектах живой природы - в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его наблюдали в устройстве вселенной, в расположении планет. В отношении з. с. находятся так же элементы геометрических фигур - пятиугольника, звезды. (Рис. 8.)
В прямоугольнике з. с. (р. 9, 10) стороны находятся в отношении з.с. Этот прямоугольник содержит в себе квадрат и малый прямоугольник з. с. (его большая сторона является малой стороной первоначального прямоугольника.)
Поэтому можно построить прямоугольник з.с. на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится прямоугольник з.с., как показано на рис. 10. 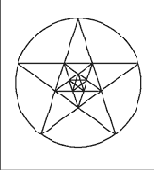
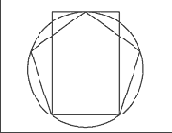
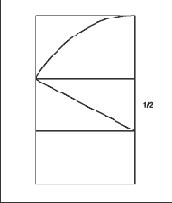
Рис. 8. Точки пересечения линий, составляющих звезду, делят их на отрезки в отношении золотого сечения.
Рис. 9. Прямоугольник приблизительно золотого сечения, построенный на основании пятиугольника.
Рис.10 Построение прямоугольника золотого сечения на основе квадрата. 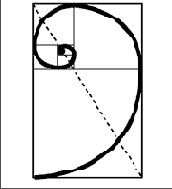
Этот малый прямоугольник подобен большому прямоугольнику, составленному из квадрата и малого прямоугольника з. с., то есть оба эти прямоугольника являются прямоугольника з. с.
Иначе говоря, если отсечь от прямоугольника з. с.. квадрат, то остается меньший прямоугольник, стороны которого опять же будут находиться в отношении з. с. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник з. с., и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют "кривая развития", "спираль жизни", ибо в ней как бы заложена идея бесконечного развития. (Рис. 11).
Бесконечное повторение прямоугольника з. с. и квадрата при рассечении прямоугольника з. с. обнаруживает повто-рение целого в его частях, что является одним из условий гармонии целого. Это свойство прямоугольника з. с. было обнаружено художниками, и они стали употреблять з. с. как способ гармонизации, способ пропорционирования. Фидий использовал з. с. при постройке Акрополя (5 век до н. э. ).
Греческие ремесленники, создавая гончарные изделия также применяли з. с. В эпоху Возрожде-ния з. с. использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли з. с. в поисках гармоничных пропорций букв (Рис12).
Прямоугольник з. с. мы встречаем и в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции з. с. позволяют красиво организовать пространство книжной страницы и разворота (рис. 13,14). 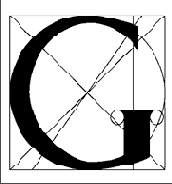
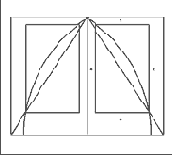
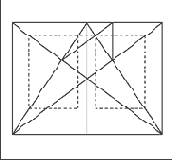
Рис. 12. Построение буквы из книги Луки Пачоли "О божественной пропорции".
Рис. 13. Схема идеальных Пропорций средневековой рукописи. Пропорции страницы 2:3, а плоскость, занятая письмом - в пропорции золотого сечения.
Рис. 14. Один из способов определения размера полосы набора при заданном формате.
Пропорционирование - приведение частей целого к единому пропорциональному строю.
В XX веке вновь возродился интерес к золотому сечению как к способу пропорционирования. Оно привлекло внимание архитекторов. Советский архитектор Жолтовский и француз Корбюзье занимались проблемами з. с. и использовали его в своей архитектурной практике. Корбюзье создал целую систему пропорционирования на основе чисел ряда золотого сечения и пропорций человеческого тела и назвал ее "Модулор", что по-латыни означает - ритмически размерять.
Модулор Корбюзье представляет собой гармонические ряды чисел, которые связаны в единую систему и предназначены для использования в архитектуре и дизайне - для гармонизации всей среды, в которой обитает человек.. Корбюзье мечтал о перестройке с помощью Модулора всей архитектурной и предметной среды. Сам он создал несколько прекрасных образцов архитектуры, но о более широком применении Модулора в существующих условиях не могло быть и речи. Модулор использовался в ряде случаев в дизайне и в графическом дизайне - при конструировании печатных изданий. На рис. 16 приводятся варианты деления прямоугольника 3:4, приведенные Корбюзье для демонстрации возможностей конструирования с помощью Модулора. 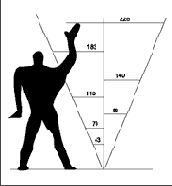
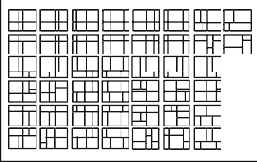
Рис. 15. Модулор (упрощенная схема).
Рис. 16. Варианты деления прямоугольника на основе Модулора.
В разработку вопроса пропорционирования и использования золотого сечения нес свой вклад Д. Хэмбидж. В 20-м году в Нью-Йорке вышла его книга "Элементы динамической симметрии". Хэмбидж исследовал динамическую симметрию, которую он обнаружил в ряде прямоугольников, с целью ее практического применения художниками в композиционном построении. Он делает попытку раскрыть секреты, которыми пользовались древние греки, добиваясь гармонического решения формы. Его внимание привлекли свойства прямоугольников, составляющих ряд, где каждый последующий прямоугольник строится на диагонали предыдущего, начиная с диагонали квадрата Ц2. Это прямоугольники Ц4, Ц5 (с меньшей стороной равной стороне квадрата, принятой за единицу). (Рис. 17). Кульминацией ряда является прямоугольник Ц5, обладающий особыми гармоническими свойствами и "родственный" прямоугольнику золотого сечения, (о нем будет сказано ниже). 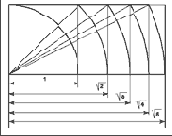
Хэмбидж рассматривает также площади квадра-тов, построенных на сторонах этих прямоугольников и обнаруживает следующую динамику: в прямоугольнике Ц2 квадрат, построенный на большей стороне, имеет площадь в 2 раза большую, чем квадрат, построенный на меньшей стороне. В прямоугольнике ЦЗ квадрат на большей стороне в 3 раза больше квадрата на меньшей стороне и так далее. Таким образом образуются динамические ряды площадей, состоящие из целых чисел. Хэмбидж утверждает, что древние греки использовали этот принцип в своих композиционных решениях. Прямоугольники динамического ряда, о котором мы говорили, являются первичными площадями в композиционной системе Хэмбиджа. Каждый из этих прямоугольников может быть разбит на отдельные части и порождать новые композиционные решения, новые темы. Например, прямоугольник Ц5 можно разбить на квадрат и два прямоугольника золотого сечения. Прямоугольник золотого сечения может быть разбит на квадрат и прямоугольник золотого сечения, а также может быть разбит на равные части, при этом обнаруживается следующая закономерность: при делении пополам он даст два прямоугольника, в каждом из которых будет по два прямоугольника золотого сечения. При делении на три части - по три прямоугольника золотого сечения в каждой трети. При делении на 4 части - по четыре прямоугольника з. с. в каждой четверти основного прямоугольника.
Среди систем пропорционирования, используемых в архитектуре, дизайне, в прикладной графике следует упомянуть системы "предпочтительных чисел" и различные модульные системы.
"Предпочтительные числа" - ряд чисел геометрической прогрессии, где каждое последующее число образуется умножением предыдущего числа на какую-нибудь постоянную величину. Числа из предпочтительных рядов используются при конструировании упаковок, в композиции рекламных плакатов. Они обеспечивают ритмическое развитие формы, их можно встретить и в построении формы античной вазы и в современной станке.
Известна система пропорционирования - так называемые "итальянские ряды", в основе которых лежат первые числа ряда Фибоначчи -2,3,5. Каждое из этих чисел, удваиваясь, составляет ряд чисел, гармонически связанных между собой 2-4, 8,16, 32, 64, и т. д. 3 - 6,12,24,48,96, 5-10,20,40,80,160.
Пропорционирование связано с понятиями соразмерности и меры. Одним из способов соизмерения целого и его частей является модуль. Модуль - размер или элемент, повторяющийся неоднократно в целом и его частях. Модуль (лат.) означает - мера. Любая мера длины может являться модулем. При строительстве греческих храмов, чтобы добиться соразмерности использовали также и модуль. Модулем мог служить радиус или диаметр колонны, расстояние между колоннами. Витрувий, римский зодчий 1 в до н. э., в своем трактате об архитектуре писал, что пропорция есть соответствие между членами всего произведения и его целым - по отношению к части, принятой за исходную, на чем и основана вся соразмерность, и соразмерность есть строгая гармония отдельных частей самого сооружения и соответствие отдельных частей и всего целого одной определенной части, принятой за исходную.
В прикладной графике модуль широко используется при конструировании книг, журналов, газет, каталогов, проспектов, всяческих печатных изданий. Применение модульных сеток помогает упорядочить расположение текстов и иллюстраций, способствует созданию композиционного единства. В основе модульного конструирования печатных изданий лежит комбинация вертикальных и горизонтальных линий, образующих сетку, делящих лист (страницу) на прямоугольники, предназначенные для распределения текста, иллюстраций и пробелов между ними. Этот прямоугольный модуль (их может быть несколько) определяет ритмически организованное распределение материала в печатном издании. Существуют сетки различного рисунка и степени сложности. А. Херлберт приводит в своей книге "Сетка" образцы модульных сеток для журналов, книг, газет (Рис. 18,19). 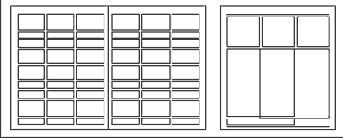
Не следует путать модульную сетку с типографской сеткой, определяющей размеры полей и формат полосы набора. Конечно, модульная сетка, постольку, поскольку имеет дело с печатными изданиями, должна учитывать размеры строк, высоту литер, пробельные элементы в типографских мерах (квадраты, цицеро, пункты), чтобы правильно располагать печатный материал на странице.
Система сеток благодаря четкой модульной основе позволяет ввести в процесс проектирования издания электронные программы.
В прикладной, промышленной графике модульную сетку применяют при конструировании всевозможных рекламных издании и, в особенности при проектировании графического фирменного стиля. Модульную сетку применяют при конструировании различных знаков, знаков визуальных коммуникаций, товарных знаков и др. (Рис. 20, 21). 
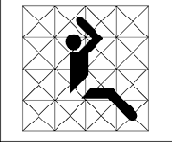
Рис. 20. Товарный знак, построенный на основе модульной сетки.
Рис. 21. Коммуникационный знак для Олимпийских игр в Мюнхене, построенный на модульной сетке.
В основу модульных сеток часто бывает положен квадрат. Квадрат очень удобный модуль. Он широко используется как модуль в современной мебельной промышленности, в особенности, при конструировании сборной мебели, "стенок".
Двойной квадрат издавна известен как модуль традиционного японского дома, где размеры комнат находились в соответствии с тем, сколько раз уложится на полу циновка-татами имеющая пропорции двойного квадрата.
В прикладной графике квадрат используется для форматов проспектов альбомов, детских книг, но он также определяет и внутреннее пространство этих изданий. Квадратный модуль может использоваться и не в квадратном формате.
Приведем пример использования квадратного модуля в квадратном формате: при трехколоночном наборе текста вся площадь, отведенная под текст и иллюстрации, делится на 9 квадратов. Если ширину колонки обозначить 1, то квадрат будет 1х1. Иллюстрации при этом могут занимать площади: 1х1, 1х2, 1хЗ, 2х2, 2хЗ, ЗхЗ, 2х1, и т. д., то есть мы будем иметь достаточно широкие возможности для комбинирования иллюстраций и текста в верстке.
В композиционной структуре произведений искусства и дизайна имеют значение пропорции прямоугольников и других геометрических фигур, в которые вписывается данное произведение или его основные части. Поэтому следует рассмотреть прямоугольники, которые нашли наиболее широкое применение благодаря своим гармоническим свойствам (о прямоугольнике золотого сечения говорилось выше). Обратимся снова к квадрату. Квадрат как конструктивная форма известен издавна. Он привлекал внимание художников Древнего мира и эпохи Возрождения.
На рисунке Леонардо да Винчи изображена связь квадрата и круга с человеческой фигурой известная еще древним, (Витрувий). Художники Возрождения - немец Дюрер, итальянец Пачоли, француз Тори, занимаясь разработкой начертания букв, исходили из формы квадрата, буква со всеми своими элементами вписывалась в квадрат (рис. 12), хотя и не все буквы приравнивались к квадрату, однако общий композиционный строй определялся квадратом. Квадрат является устойчивой, статичной фигурой. Она ассоциируется с чем-то неподвижным, завершенным. В Древнем мире у некоторых народов изображение квадрата было связано с символикой смерти. (В этой связи интересно заметить, что пропорции квадрата в природе встречаются в формах неживой материи, у кристаллов). Благодаря своей статической завершенности квадрат используется в прикладной графике, в области визуальных коммуникаций наряду с формой круга как элемент, фиксирующий внимание, а также для ограничения пространства, на котором сосредоточена информация. 
Помимо прямоугольника золотого сечения и квадрата, наибольший интерес для нас представля-ют прямоугольники Ц2 и Ц5. Древние греки эпохи классики предпочитали именно эти прямоугольники. Хэмбидж утверждает, что 85% произведений греческого классического искусства построено на прямоугольнике Ц5. Чем интересен этот прямоугольник? Будучи разделенным по вертикали и по горизонтали на две части, он восстанавливает свои пропорции. Прямоугольник этот можно расчленить на квадрат и два малых прямоугольника золотого сечения. Кроме того, в нем просматриваются два прямоугольника золотого сечения, перекрывающие друг друга на величину квадрата. Оставшаяся часть тоже представляет собой прямоугольник золотого сечения. Таким образом, прямоугольник Ц5 обнаруживает ритмические свойства. В нем возникает красивая симметрия (малый прямоугольник з. с. +квадрат+малый прямоугольник з. с.)(рис 22).
Прямоугольник Ц2 также находит широкое при-менение, в особенности в области прикладной графики. Он используется как формат бумаги для деловой документации, поскольку обладает удивительным свойством, - при делении пополам он не меняет своих пропорций. При делении образуется ряд подобных прямоугольников, гармонически связанных между собой единством формы. (Рис. 23, 24, 25). На рис. 26 приводится изображение прямоугольников, используемых при композиционном построении благодаря гармоническим отношениям их сторон. 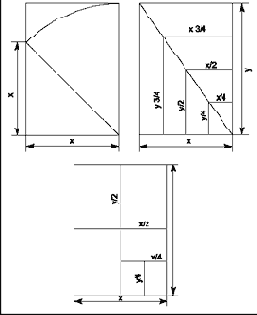
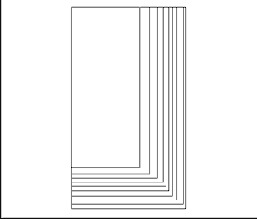
Рис. 23, 24, 25. Пропорции сторон в прямоугольнике Ц2, использованные в стандарте Порстмана.
Рис. 26. Гармонические отношения сторон в прямоугольниках.
Хэмбидж приводит композиционную схем у греческой чаши для питья из бостонского музея: чаша вписывается (без ручек) в горизонтально вытянутый прямоугольник Ц5. Диагонали двух прямо-угольников золотого сечения, перекрывающих друг друга на квадрат, пересекаются в точке, через которую проходит граница между чашей и ее ножкой. Ширина основания ножки равна высоте чаши и равна стороне квадрата, находящегося в центре прямоугольника Ц5. Ножка вписывается в два малых прямоугольника з. с., отсеченных от квадрата линией, горизонтальной к основанию прямоугольника Ц5 и проходящей через точку пересечения двух диагоналей больших прямоугольников з. с.
В современном художественном конструировании прямоугольник Ц5 также находит широкое применение. Мы его встречаем в пропорциях автомашин, станков и других изделий. В прикладной графике - в форматах проспектов, буклетов, упаковок, в изобразительном искусстве, в монументальном искусстве, - в пропорциях картинной плоскости, в композиционном строе картины.
Ниже приводятся числовые отношения прямоугольников Ц2, ЦЗ, Ц4, Ц5 к их обратным числам, с которыми они находятся в гармоническом отношении. (Обратным числом называется число, полученное при делении единицы на данное число). Ес-ли принять меньшую сторону прямоугольника за единицу, то для прямоугольника число (соответствующее большей стороне прямоугольника) =1,4142, а обратное число =0,7071, для прямоугольника ЦЗ число=1,732, обратное число=0,5773, для прямоугольника Ц4 число=2, обратное число =0,5, для прямоугольника Ц5 число=2,236, обратное число=0,4472, для прямоугольника з. с. число= 1,618, обратное число=0,618.
На основе прямоугольника Ц2 была проведена стандартизация и унификация форматов книг, бумаг, деловой документации, открыток, плакатов, папок и других объектов, связанных с прикладной графикой. Этот стандарт, известный как стандарт доктора Порстмана был принята 17 европейских странах. В основу стандарта был положен формат 841Х1189мм и площадью в 1м2. От него выведены остальные форматы, составляющие его доли (рис. 27) 1м'-841Х1189мм. 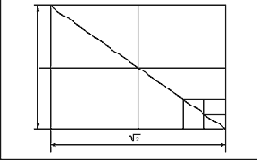
1/2м2-594Х841мм
1/4м2-420Х594мм
1/8м2 - 297Х420мм (двойной лист)
1/16м2- 21 OX 297мм (лист для деловой переписки, бланков)
1/32м2- 148Х210 мм (поллиста для деловой переписки, бланков)
1/64м2- 105Х148мм (почтовая открытка) 1/128м2- 74Х105мм (визитная карточка)
Стандартом предусмотрены и дополнительные форматы 1000Х1414 и 917Х1297 и их доли. Для конвертов предлагаются, размеры 162Х229 и 114Х162 (Стандарт приведен не полностью).
Поскольку обращение с деловыми бумагами, документацией подразумевает необходимость иметь не только соответствующие им по размеру и формату конверты и папки, но и емкости, в которых хранится документация, отсюда возникает необходимость в соответствующей мебели столах, шкафах, полках. Размеры и пропорции мебели, в свою очередь, подсказывают и характер интерьеров помещений. Таким образом возникает целостная система гармонизованных элементов интерьера, подчиненная единому модульному принципу.
Пропорциональные отношения должны существовать не только между отдельными частями целого, но и между предметами, составляющими группы объектов, связанных единым стилем, функциональной задачей. Например, между объектами, входящими в систему фирменного стиля.
Предметы, окружающие человека, должны быть гармонизованы не только по отношению друг к другу, но и связаны с человеком единой мерой, с физическим его строением. Зодчие древности считали, что отношение частей архитектуры друг к другу и к целому должно соответствовать частям человеческого тела, их отношениям. Таким же образом Модулор Корбюзье исходит из размеров человеческого тела и из отношений золотого сечения в нем, (расстояние от земли до солнечного сплетения и расстояние от солнечного сплетения до макушки составляют крайнее и среднее отношения золотого сечения) (Рис. 15).
Масштабные отношения между вещами, предметным окружением и человеком выступают как средство гармонизации, ибо масштаб является одним из проявлений соразмерности, устанавливающим относительные размеры между человеком и предметом - в архитектуре, в дизайне, в прикладном искусстве, в частности, в прикладной графике, в искусстве книги Так, размеры и форматы плакатов и любых объектов, служащих целям визуальной коммуникации - вывесок, дорожных знаков и т. д., а также их композиционное решение всегда избираются в зависимости от назначения и от условий эксплуатации, а значит и в соответствующих масштабных отношениях. То же самое касается и области книжного оформления и всевозможной печатной рекламы и упаковки.
Симметрия. В пропорции и соразмерности проявляются количественные отношения между частями целого и целым. Греки к ним присоединяли и симметрию, рассматривая ее как вид соразмерности, - как ее частный случай - тождество. Она, как и пропорция, почиталась необходимым условием гармонии и красоты. 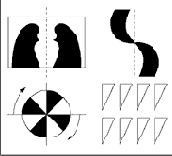
Симметрия основана на подобии. Она означает такое соотношение между элементам и, фигурами, когда они повторяют и уравновешиваютдруг друга. В математике под симметрией подразуме-вается совмещение частей фигуры при перемещении ее относительно оси или центра симметрии. Существуют различные виды симметрии. Простейший вид симметрии - зеркальная (осевая), возникающая при вращении фигуры вокруг оси симметрии. Симметрия, возникающая при вращении фигуры вокруг центра вращения называется центральной. Наивысшей степенью симметрии обладает шар, так как в центре его пересекается бесконечное множество осей и плоскостей симметрии. Абсолютная, жесткая симметрия характерна для неживой природы - кристаллов (минералов, снежинок). Для органической природы, для живых организмов хара-терна неполная симметрия (квазисимметрия), (например, в строении человека). Нарушение симметрии, асимметрия (отсутствие симметрии) используется в искусстве как художественное средство. Небольшое отклонение от правильной симметрии, то есть некоторая асимметричность, нарушая равновесие, привлекает к себе внимание, вносит элемент движения и создает впечатление живой формы. Различные виды симметрии обладают различным воздействием на эстетическое чувство: зеркальная симметрия - равновесие, покой, винтовая симметрия вызывает ощущение движения. Хзмбидж причисляет все простые геометрические фигуры к статичной симметрии, (разделяя все виды симметрии на статичные и динамичные), а к динамичной симметрии относит спираль. В основе статичной симметрии часто лежит пятиугольник (срез цветка или плода) или квадрат (в минералах). В искусстве строгая математическая симметрия используется редко.
Симметрия связана с понятием середины и целого. В древнегреческой философии и искусстве понятие "середины, центра связано с представлением о цельности бытия. Середина - "избегание крайностей" (Аристотель) - означает принцип уравновешенности "Везде грек видел нечто цельное. А это и значит, что он прежде всего фиксировал центр наблюдаемого или постороннего предмета. Без понятия "середины" немыслимо античное учение о пропорциях, мере, симметрии или гармонии". 
Гармония - понятие диалектическое. По древнегреческой мифологии Гармония - дочь бога войны Арея и богини любви и красоты Афродиты, - то есть, в ней слиты противоположные, враждующие начала. Поэтому понятие гармонии включает в себя контраст как необходимое усло-вие. Контраст способствует многообразию и разнообразию, без которых немыслима гармония. "Гармония есть единение многого и согласие несогласного" (Филолай). Это знали древние. Художник ХVIII в. Хогарт находил, что сущность гармонии в единстве и разнообразии. Он преклонялся перед волнообразной линией, которую считал "линией красоты и грации", потому что она является конкретным воплощением единства и разнообразия. Без разнообразия невозможна красота. Однообразие утомляет. В смене противоположного проявляется диалектическая закономерность - отрицание отрицания. В зримых образах искусства она выражается через ритм и контраст. Смысл гармонии в обуздании хаоса. Но она осуществляет это через борьбу противоположных начал. Объединяя противоположные начала, гармония уравновешивает их, вносит меру и согласие, упорядочивает и в награду получает красоту.
Гармония - эстетическая категория.
Симметрия, пропорции, ритм, контраст, цельность - образующие гармонию объективно связаны с природой, с движением и развитием материи. Наши эстетические представления тесно связаны с этими понятиями. Однако, социальное бытие человека в разные эпохи под разным углом зрения рассматривало категории гармонии и это определяло их роль в общественной жизни и в искусстве Представление о прекрасном раз-вивалось, менялось. Гармония стала рассматриваться не как количественный, а как качественный принцип, объединяя физическое и духовное начала. Если древние греки считали прекрасным только упорядоченное и всякое нарушение симметрии и пропорций находили безобразным, то в последующие эпохи проявления прекрасного стали обнаруживать и в нарушении порядка, в диссонансах, в кажущейся дисгармонии, ибо они свойственны жизни и, следовательно, являются частью какой-то иной гармонической системы, в которой обретают логику и смысл. "Прекрасное - есть жизнь",- писал Чернышевский. И она не стоит на месте. Появления гармонии в природе и жизни шире, чем это может охватить любой канон, любая гармоническая система. И человечество никогда не перестанет искать новых гармонических отношений, сочетаний, искать проявления иных гармонических закономерностей. Однако, это не значит, что классическая гармония потеряла свое значение. То, что уже открыто, те найденные закономерности, их математическое обоснование, остаются вечным достоянием человечества, из которого будут черпать все последующие поколения.
Гармония - эстетическая категория, и ее нельзя сводить к понятию пропорции или симметрии. Она включает в себя многоплановые отношения человека с миром, социальные отношения, свя-зана с представлением о нравственных ценностях. Гармонически развития личность - цель коммунистического общества, в котором должна осуществляться высшая гармония чело века, общества и природной среды. Но это понимание гармонии невозможно без той первоначальной ступени, того основания, которое было заложено в "учении о гармонии" древних, без понимания единства мира, проявляющегося в гармонических отношениях чисел, при родных форм, без понимания диалектики природы и диалектического начала гармони и, без понимания роли гармонии в жизни и в искусстве.
Стремление к гармоничным формам существования естественно для человека. Внесение гармонического начала в искусство - необходимость, вызванная потребностью реалистического отображения действительности с целью ее освоения, познания и верного отражения ее в художественной форме, предназначенной для эмоционального и целенаправленного функционального ее воздействия.
Глава 1: Часть 1, 2 
![]() Часть 4
Часть 4 
![]() Глава 2: Группа 1-5
Глава 2: Группа 1-5 
сделано для http://www.natahaus.ru/
